一所懸命HWデザイナーのふりをやっとる現代のC++が大嫌いなSWの開発者。FPGAのGPUとレトロな家庭用ゲーム機を作ること、うちの猫(ニュートリノ+コスモス)、お箏の演奏、ゲーム開発、抹茶+和菓子がめっさ好きやねん。tweetsは私個人の意見で、会社を代表するものやない
Part 0: The Problem Statement
In the current design, sixteen rasterizers operate on 8×8 pixel tiles. The two problems we need to solve here are 0) how to work out what tiles a triangle intersects, and 1) how to dispatch those tiles to the rasterizers
Each rasterizer is secretly just a 16-wide SIMD, meaning all 8×8=64 pixels in a tile are processed in 64/16 = 4 clocks. But you can see the problem with this, right? If we dispatch one tile per clock, any particular rasterizer gets a new tile every 16 clocks, meaning they will be sitting around, bored out their minds, 75% of the time
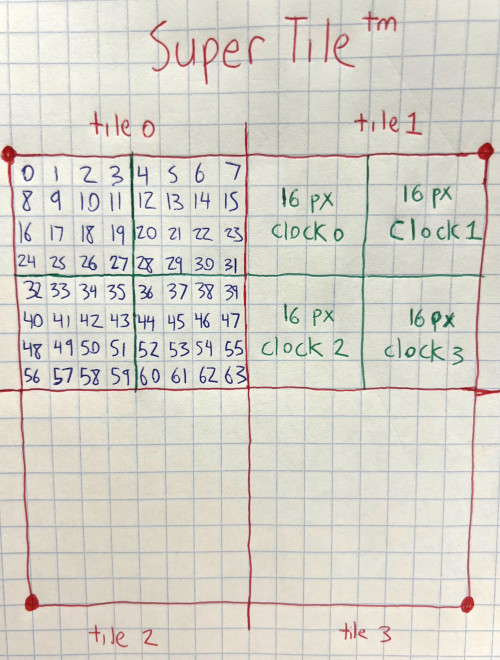
The simplest solution is to dispatch four tiles at a time, in some kind of 16×16 pixel SuperTiletm (name not final) that all share a texture cache. This works great for large-ish triangles, but can operate around 50% efficiency for very long and thin triangles, and 25% efficiency for very small triangles
Maybe I’ll have time to address these inefficiencies in a future post, but for now the mandate is to keep things as dumb and simple as possible. Or maybe I can just throw “oi, draw better triangles!” in the hardware docs somewhere visible?
Part 1: Prerequisites For The Non Mathy
Don’t worry, I’m not looking to make you relive your high school linear algebra class trauma. I just want to remind you about the bare minimum needed to understand the triangle edge functions we’ll be using. If you are looking for a proper maths teacher, go watch some videos from the absolutely brilliant Freya Holmer. No one on the planet is better at explaining things deeply and intuitively. But since I am a garbage explainer, the best I can manage is the following hand-drawn kindergarten art
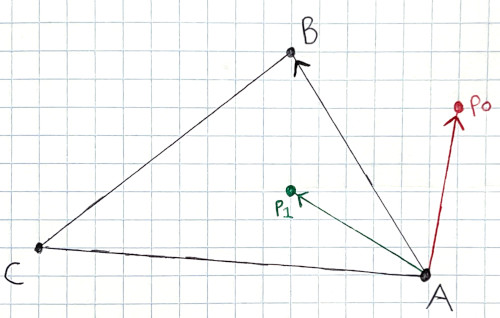
To know if a triangle intersects a tile, we first need a way to know if some point is inside the triangle. In the above image, its visually obvious that p0 is outside and p1 is inside, but we need a way to calculate this
Cross products aren’t just used for passing Naughty Dog applicant interviews! Apparently they can also be used for other things, such as finding a vector that is perpendicular to the input vectors. In our case, the input vectors are in the XY plane, and so the result direction will be entirely along the Z axis
Let’s look at the edge from vertex A to B, which is (B – A). We want to take the cross product of that with the vector from A to p0, or (p0 – A). The resulting magnitude of (B – A) x (p0 – A) is related to the signed perpendicular distance from p0 to the triangle edge AB such that values of zero means p0 is on the edge, negative values means p0 is outside of the edge, and positive values means p0 is inside the edge. Because the result is entirely along the Z axis, we only need to verify the sign bit of Z for edges AB, BC, CA is all zero to know the point is inside the triangle
Calculating (B – A) x (p0 – A) would be expensive and annoying… if we had to. But because the Z component of all points is zero, the cross product simplifies to the 2D determinant. And so
; (B-A) x (p0 - A)
det = (Bx - Ax) x (p0y - Ay) - (By - Ay) x (p0x - Ax)
; factoring p0 out
p0y(Bx - Ax) - p0x(By - Ay) - Ay(Bx - Ax) + Ax(By - Ay)
; stuff that doesn't depend on p is constant for the triangle
offs = -Ay * (Bx - Ax) + Ax * (By - Ay)
; the remaining bits are the function increments as p changes
xinc = By - Ay
yinc = Bx - Ax
; new final result
cross = py * yinc - px * xinc + offsRight, that probably looks more complicated than it needs to be, but it will make rasterization easier later on. Offs can be calculated once per triangle, and factoring the rest into xinc and yinc means we can evaluate the edge functions as we incrementally walk pixel by pixel across the screen simply by repeatedly adding the X and Y offsets. Yay for linear functions!
This post won’t cover how the edge functions are calculated. That’s a different hardware block! It also won’t cover how to generate barycentrics. That is also a different block! I just wanted to make sure you understand why you can look at the edge function sign bits to determine if a point is inside a triangle
Part 2: Basic Distribution
The core of tile distribution is this: for each tile row, we need to find the minimum (leftmost) tile that the triangle intersects, and then move right until the current tile no longer intersects the triangle. These intersecting tiles are then given to the rasterizers for… rasterization?
*sigh* I explored alot of “creative” ideas to avoid having to write a triangle walker. I spent a month falling down a SuperTiletm-shaped coarse rasterization hole, trying to encode reciprocals in a LUT5 and then using the original LSBs to try to correct the arising precision issues. The results were dramatically better than my second GPU’s AABB method, but there were always bad edge cases where too many empty tiles ended up getting dispatched
For some reason, I had convinced myself either the area cost of a proper walker would be too high, or that I wouldn’t be able to close timing without lowering the clock frequency due to mux/datapath length issues. But after obsessing for a week or two, I settled on an implementation idea I thought maybe might have reasonable chance of working
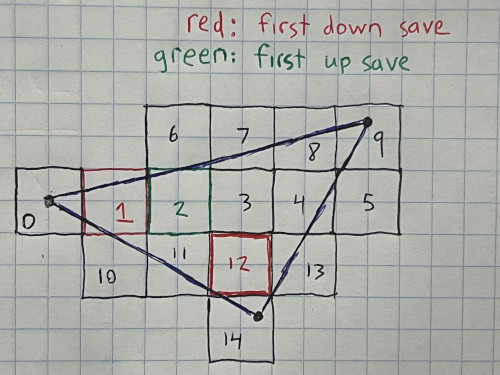
The high level walking algorithm isn’t very original. Find the leftmost vertex, and initialise the current tile to the vertex’s 16×16 AABB, (0) in the image above. Move the tile right until you find the last valid tile in the row (5). Along the way, also check above and below the current tile, and save the first valid up (2) and down (1) positions for the row. When you get to the end of a row, move to the saved up position (6) if it exists, and repeat until you hit the top of the triangle. When that’s done, jump to the first saved down position (10) and repeat the whole process, but this time moving down. That way, you can walk the entire triangle, 16×16 blocks at a time, without the waste of dispatching all the empty tiles in the triangle’s AABB
Updating Tile Position
A tile has four corners at which the three edge functions are evaluated, and we need to work out some rules for updating them that minimise the multiplexer inputs and avoids unnecessary adder logic
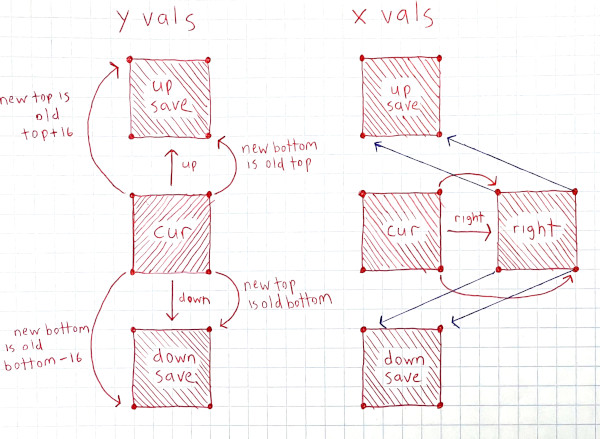
the lower left and upper left points, a0 and a1 respectively, are called anchor points, and they are registered in flip flops. Upper right and lower right points are calculated in combinational logic by adding the edge function x increments to the anchor points. If a tile could only move right, it would be enough to say that the new left points can reuse the old right points values, but because a tile can also move up and down, things are more complicated
Looking at the anchor points alone, there are seven possible values: The initialised value, the saved up position (next row when traversing up), the saved down position (next row when traversing down), the first down position (jump here after finishing the upwards walk), the right position, the immediate up, and the immediate down. The immediates aren’t strictly necessary, but are an optimisation meant to avoid needing one empty tile at the end of each row. Anyway, that’s too many values!
Ideally we’d want that to be three possible values in order to take advantage of LUT6 secretly being implemented as two LUT5s. However four possible values would also be acceptable as that would allow the tools to use a LUT6 as a mux with four input bits and two select bits. So what can we do? First, because the init value is only used in the kDistStateInit state, init and the first down position can reuse the same storage. The downside is that that we then need to return to the init state for one clock when transitioning from walking up to walking down. OK, that’s down to six possible values. What next?
Well, above I said that a0 and a1 were the lower left and upper left anchors respectively. However, when transitioning from walking up to walking down, if we negate the edge function y increments and allow the anchor points to swap such that a0 becomes the upper left and a1 becomes the lower left, then the up and down logic becomes identical. Saved up position and saved down position merge into next_row_saved_pos0, and the immediates are similarly merged. That gets us down to four points!
Then it’s sufficient to use three bits, {is_init, is_right_tile_valid, was_next_row_already_found} to build a mux select to select between the four values
genvar gi;
generate
for (gi = 0; gi < kNumTriEdges; ++gi) begin
// two right points are calculated from the two left points
assign anchor0_r[gi] = anchor0[gi] - input_port_xincs[gi];
assign anchor1_r[gi] = anchor1[gi] - input_port_xincs[gi];
end
endgenerate
...
// same as above, but tests the tile to the right, i.e. next tile in the row
// edge because I'm checking if the next tile (not the current tile) is valid.
// If I want to add an empty tile at the end of each row I should check all 4
//points because I want to stop when the current tile is invalid, not the next
assign is_right_tile_valid =
// at least one vert inside A
(`MSB(anchor0_r[kTriEdgeA]) == 1'b0 | `MSB(anchor1_r[kTriEdgeA]) == 1'b0) &
// at least one vert inside B
(`MSB(anchor0_r[kTriEdgeB]) == 1'b0 | `MSB(anchor1_r[kTriEdgeB]) == 1'b0) &
// at least one vert inside C
(`MSB(anchor0_r[kTriEdgeC]) == 1'b0 | `MSB(anchor1_r[kTriEdgeC]) == 1'b0);
...
unique case ({is_init, is_right_tile_valid, was_next_row_already_found}) inside
3'b1??: begin // in the idle state, so always init_or_down_pos0
for (int e = 0; e < kNumTriEdges; ++e) begin
anchor0[e] <= init_or_down_pos0[e];
anchor1[e] <= init_or_down_pos1[e];
end
end
3'b000: begin // right not valid (end of row), no saved next row, use forwarded immediate
for (int e = 0; e < kNumTriEdges; ++e) begin
anchor0[e] <= anchor1[e];
anchor1[e] <= anchor1[e] + yoffs[e];
end
end
3'b001: begin // right not valid (end of row), valid saved next row, use it
for (int e = 0; e < kNumTriEdges; ++e) begin
anchor0[e] <= next_row_saved_pos0[e];
anchor1[e] <= next_row_saved_pos1[e];
end
end
3'b01?: begin // right is valid, so A0 + xoffs
for (int e = 0; e < kNumTriEdges; ++e) begin
anchor0[e] <= anchor0[e] - input_port_xincs[e];
anchor1[e] <= anchor1[e] - input_port_xincs[e];
end
end
endcaseIntersection Detection
If walking depends on knowing if the tile to the right, above, and below are valid, we need a cheap way to determine it. This turns out to be pretty trivial. Let’s say you want to know if the next tile to the right is valid. Look at the rightmost points (p0 and p1 below), and make sure that for every triangle edge, at least one of p0 or p1 is inside the edge
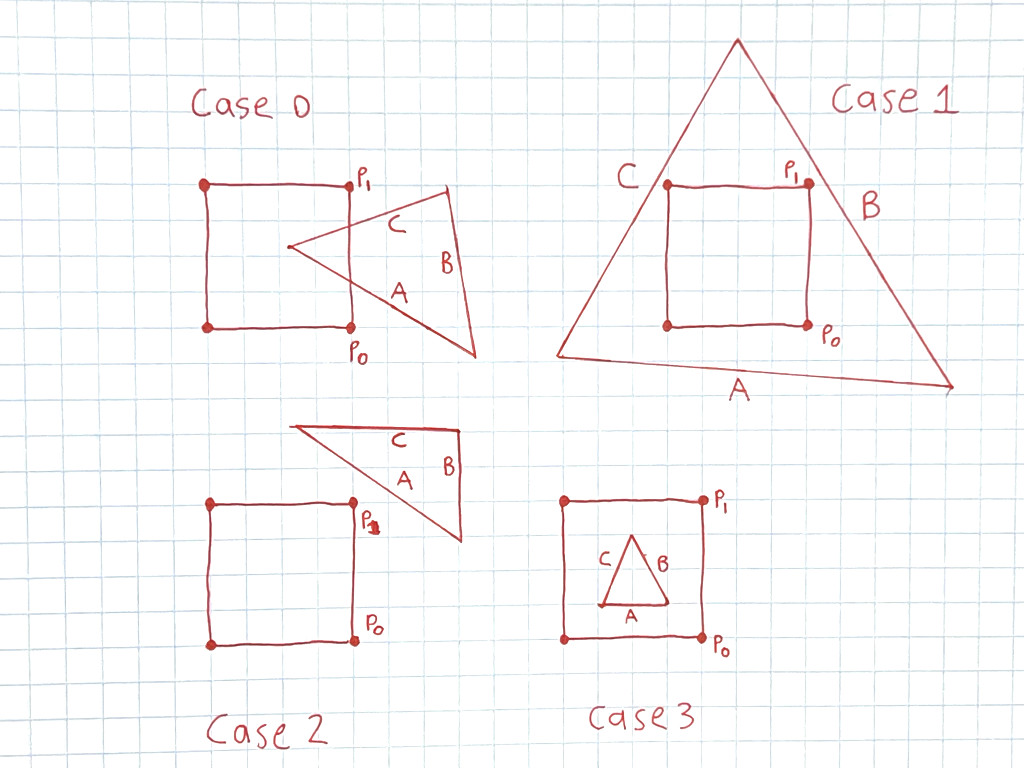
In case 0, p1 is inside edge A, both points are inside edge B, and p0 is inside edge C, so the triangle intersects the tile to the right. In case 1, all points are inside the triangle, so the up, right, and down tiles all need to be processed
Case 2 should never occur as the current tile starts valid and never moves to an invalid position, but I am including it for funsies. In case 2, both points are inside edges B and C, but because no point is inside edge A, the intersection test correctly fails. Technically case 3 doesn’t work at all, but because we always start on a valid tile and use the intersection tests to determine if the next tile is valid, this still produces the correct result
False Positives
It may seem at first like false positives could happen. Take for example:
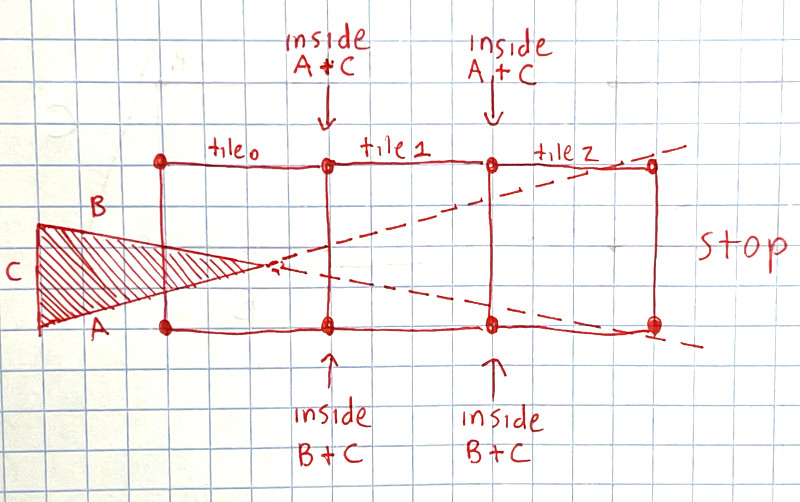
Tile 0 is the current tile, and we need to determine whether to move right to tile 1. The top vert is inside edges A and C, and the bottom vert is inside B and C, and so an intersection is reported and we move to tile 1. We have the same problem with tile 2, but eventually the false positives stop. The natural triangle bounding box stops this case from happening, since tile 1 is outside the bounding box, and therefore we’d never move to it
Results
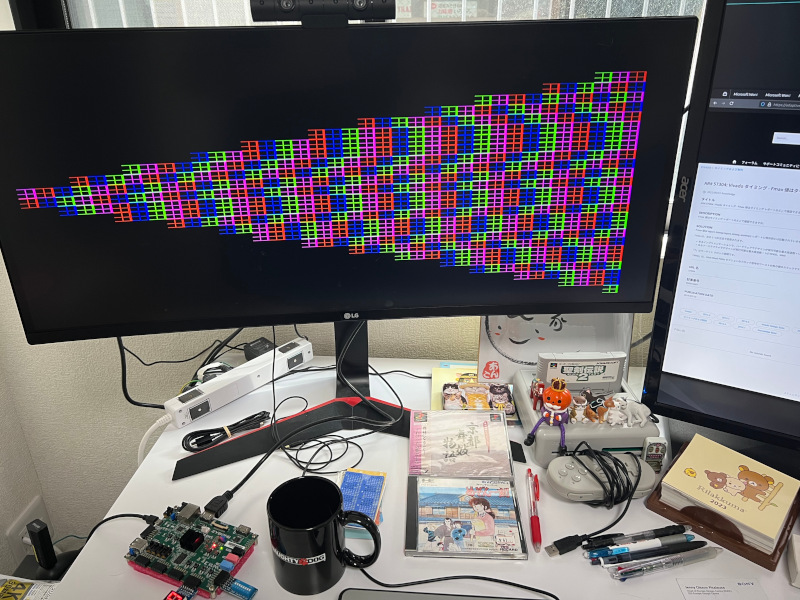
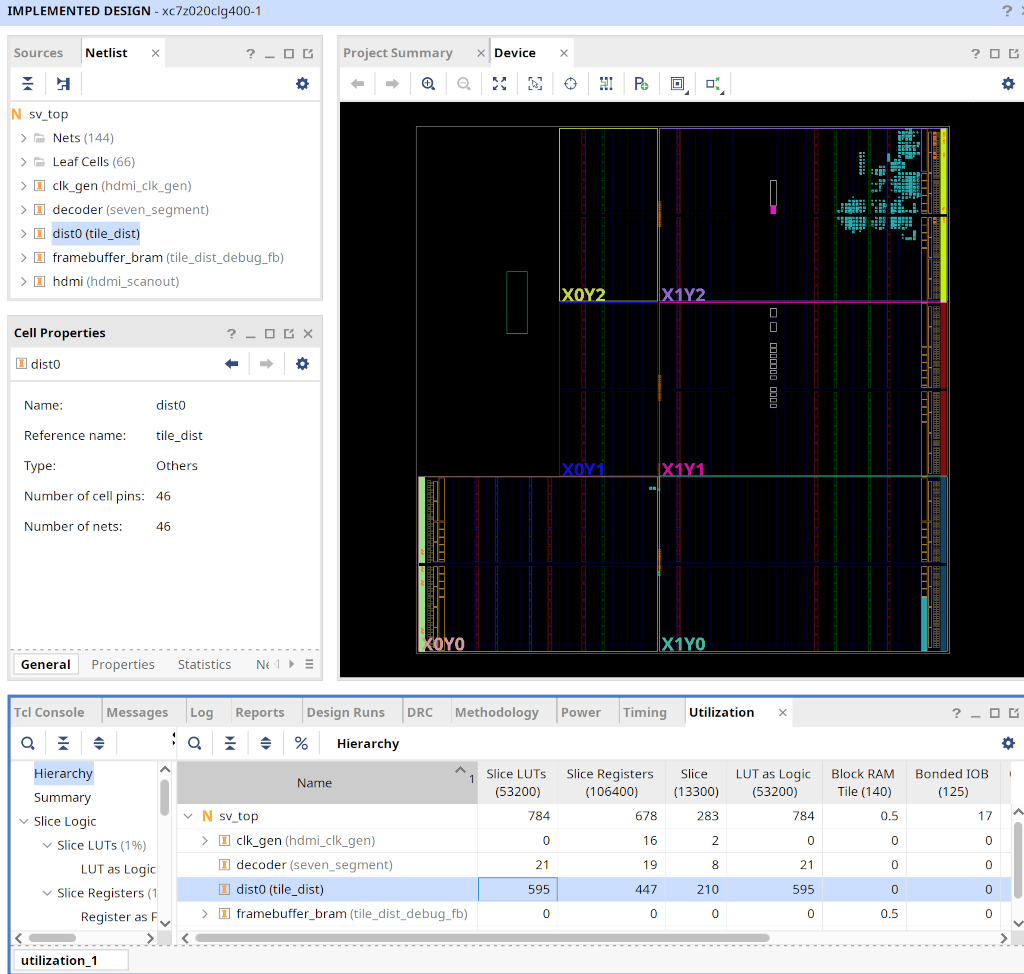
Not gonna lie, I’m feeling uncharacteristically positive about this. I spent about a month optimising for area and timing, and in the end was able to end up with something that, including debug colour generation logic, uses 595/53200 (1.1%) of the total LUTs, 447/106400 (0.42%) of the total flops, and closes timing at 200MHz. Vivado doesn’t report Fmax in the timing report, so I’m not sure how high I could take that without a very drawn out trial and error process
There are further optimisations to be done, but for now I feel pretty confident that I won’t need to switch back to the old dark days of AABB tile distribution. OK then, onward to the next gen rasterizers!